Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?

Toán học là lĩnh vực nghiên cứu các con số, mặt phẳng, không gian, và hình học. Nó đóng vai trò thiết yếu trong cuộc sống hàng ngày, từ các phép toán cơ bản như cộng, trừ, nhân, chia cho đến việc hiểu biết về các hình học khác nhau. Bài viết này của Mytour sẽ giải thích về hình chóp tứ giác đều, các tính chất của nó và số lượng mặt phẳng đối xứng của hình này.

1. Hình chóp tứ giác đều

Hình chóp tứ giác là một khối hình học ba chiều, được tạo ra từ một tứ giác đáy và một điểm nằm ngoài mặt phẳng của tứ giác đó, cùng với các đoạn thẳng nối điểm này đến các đỉnh của tứ giác đáy. Hình chóp tứ giác có một đỉnh và một đáy là tứ giác, với các cạnh nối từ đỉnh đến các đỉnh của đáy gọi là cạnh bên. Nó có thể là chóp đều hoặc không đều, tùy vào hình dạng và độ dài của các cạnh và mặt. Trong hình học, hình chóp là một đa diện được hình thành từ một điểm trên mặt phẳng đa giác và một điểm khác, gọi là đỉnh. Các cạnh cơ sở và đỉnh tạo thành các mặt bên hình tam giác.

Hình chóp đều (hay hình chóp đa giác đều) là loại hình chóp có đáy là một đa giác đều và khi chiếu đỉnh xuống đáy, điểm chiếu trùng với tâm của đáy. Đặc điểm của hình chóp đều là đáy là một đa giác đều và tất cả các cạnh bên đều bằng nhau.

1.1. Định nghĩa hình chóp tứ giác đều

Hình chóp tứ giác đều là loại hình chóp có đáy là hình vuông và đường cao của chóp đi qua trung điểm của đáy, nơi giao nhau của hai đường chéo của hình vuông. Đây là một hình chóp tứ giác đặc biệt, trong đó đáy là một tứ giác đều và tất cả các cạnh bên đều có chiều dài bằng nhau, tạo thành các tam giác cân. Đối với hình chóp tứ giác đều, đường cao, đường trung tuyến, và đường phân giác của đáy đều hội tụ tại một điểm duy nhất gọi là trọng tâm.

Với đáy là đa giác đều và các cạnh bên đều bằng nhau, ta có thể chứng minh rằng hình chiếu của đỉnh trên đáy chính là tâm của đa giác đáy. Các tam giác vuông được tạo thành (với một đỉnh là đỉnh chóp, một đỉnh là hình chiếu của đỉnh trên đáy, và đỉnh còn lại là các đỉnh của đa giác đáy) là bằng nhau nhờ có cạnh góc vuông chung (đường cao từ đỉnh xuống đáy) và các cạnh huyền bằng nhau (cạnh bên của đa giác). Do đó, hình chiếu của đỉnh hình chóp trên đáy chính là điểm giao nhau duy nhất của các đường trung trực của các cạnh đa giác đáy, hay chính là tâm của đáy.

1.2. Các đặc điểm của hình chóp tứ giác đều

+ Đáy của hình là một hình vuông;

+ Các cạnh bên đều có chiều dài giống nhau;

+ Các mặt bên đều là các tam giác cân;

+ Chân đường cao trùng với tâm của mặt đáy, nơi giao nhau của hai đường chéo;

+ Tất cả các góc giữa cạnh bên và mặt đáy đều bằng nhau;

Tất cả các góc được tạo bởi các mặt bên và mặt đáy của hình chóp đều bằng nhau.

Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?

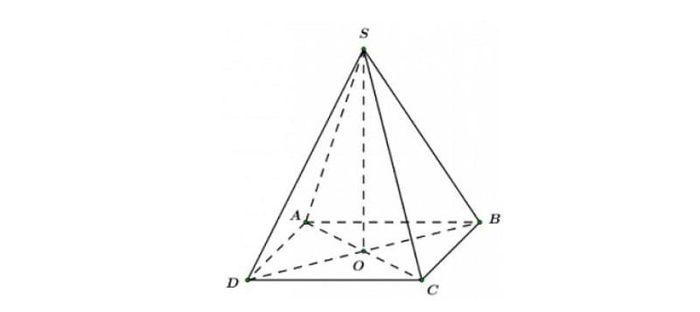
Nhìn vào hình, nếu I là trung điểm của AD, K là trung điểm của BC, M là trung điểm của AB và N là trung điểm của CD.

Hình chóp tứ giác đều có 4 mặt phẳng đối xứng, cụ thể là (SAC), (SBD), (SIK), (SMN). Đây là hình chóp có đáy hình vuông với đường cao đi qua tâm của đáy (giao của hai đường chéo của hình vuông).

Ví dụ: Hình chóp tứ giác đều S.ABCD có ABCD là hình vuông với tâm O.

SO vuông góc với mặt phẳng (ABCD).

SA = SB = SC = SD.

Góc giữa SA và mặt phẳng (ABCD) bằng góc giữa SB và mặt phẳng (ABCD), cũng bằng góc giữa SC và mặt phẳng (ABCD), và bằng góc giữa SD và mặt phẳng (ABCD).

2. Mặt phẳng đối xứng trong các khối hình thường gặp

Định nghĩa: Một mặt phẳng (P) được gọi là mặt phẳng đối xứng của hình (H) nếu phép đối xứng qua (P) làm hình (H) trùng với chính nó.

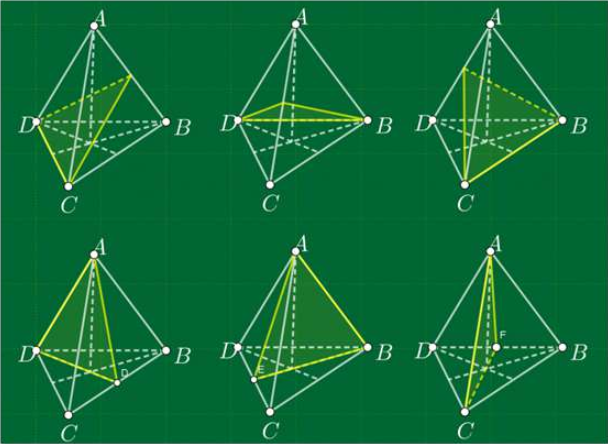
Mặt phẳng đối xứng của tứ diện đều

Tứ diện đều có 6 mặt phẳng đối xứng. Mỗi mặt phẳng này đi qua một cạnh và trung điểm của cạnh đối diện.

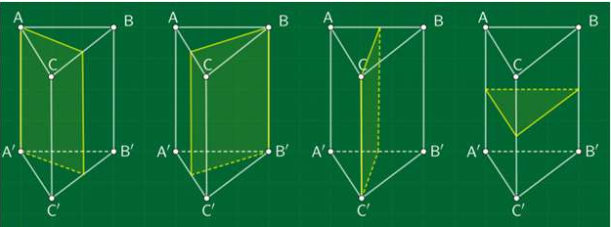
Mặt phẳng đối xứng của lăng trụ tam giác đều

+ 3 mặt phẳng: đi qua 1 cạnh bên và trung điểm của 2 cạnh đáy.

+ 1 mặt phẳng: đi qua trung điểm của 3 cạnh bên

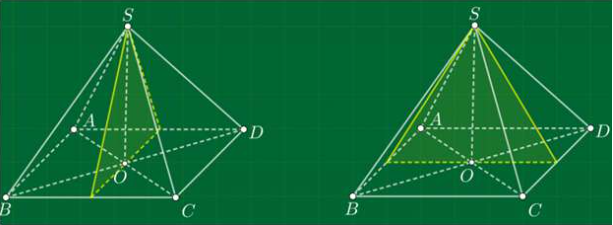
Các mặt phẳng đối xứng của hình chóp tứ giác đều

+ 2 mặt phẳng: đi qua đỉnh và 1 đường chéo của đáy.

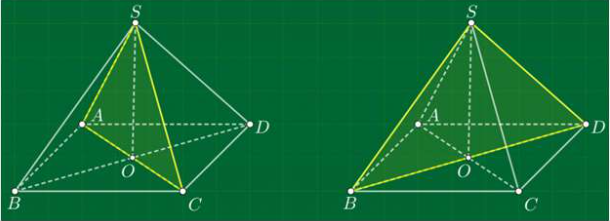
+ 2 mặt phẳng: đi qua trung điểm của 2 cạnh đáy đối diện và đỉnh.

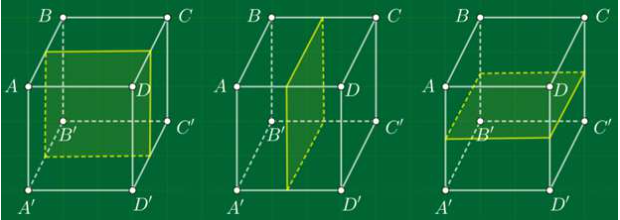
Các mặt phẳng đối xứng của hình lập phương

+ 3 mặt phẳng: mỗi mặt phẳng chia khối lập phương thành 2 khối chữ nhật.

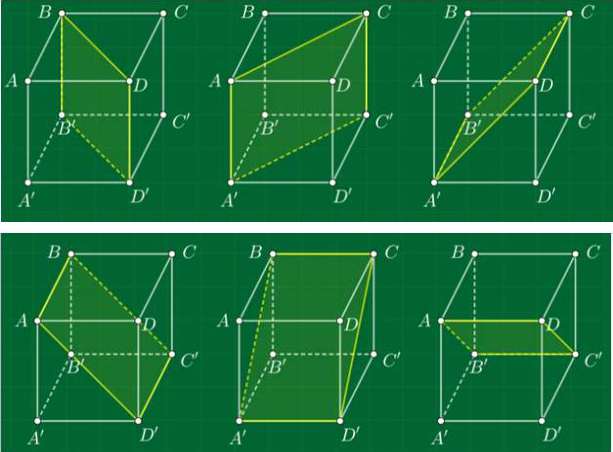
Hình chóp tứ giác đều có 6 mặt phẳng đối xứng: mỗi mặt phẳng chia khối lập phương thành hai phần giống hệt nhau.

Các mặt phẳng đối xứng của hình hộp chữ nhật bất kỳ

Hình hộp chữ nhật với 3 kích thước khác nhau chỉ có 3 mặt phẳng đối xứng, giống như các mặt phẳng của hình lập phương đã nêu. Các mặt phẳng này đi qua trung điểm của các cặp cạnh song song và chia hình hộp chữ nhật thành hai phần giống hệt nhau.

Nếu hình hộp chữ nhật có hai chiều bằng nhau và một chiều khác biệt, thì nó có thêm 2 mặt phẳng đối xứng. Tổng cộng có 5 mặt phẳng đối xứng.

Các mặt phẳng đối xứng của hình bát diện đều

Mặc dù ít gặp hơn, hình bát diện đều có 9 mặt phẳng đối xứng. Trong đó, 3 mặt phẳng chia bát diện đều thành hai khối chóp tứ giác đều với các cạnh bằng nhau, còn 6 mặt phẳng đối xứng còn lại đi qua các cặp đỉnh đối diện, mỗi cặp có 2 mặt.

3. Một số công thức liên quan đến hình chóp tứ giác đều và các bài tập ứng dụng

3.1 Các công thức liên quan

• Diện tích của hình chóp tứ giác đều

+ Diện tích xung quanh của hình chóp đều được tính bằng cách nhân nửa chu vi đáy với chiều cao của trung đoạn:

Sxq = p.d (trong đó p là nửa chu vi đáy, d là chiều cao trung đoạn)

+ Diện tích toàn phần của hình chóp được tính bằng tổng của diện tích xung quanh và diện tích mặt đáy.

Dưới đây là công thức cần nhớ:

Stp = Sxq + S (trong đó S là diện tích của đáy)

• Thể tích của hình chóp tứ giác SABCD là:

V = 1/3 x SABCD x SO

Trong đó: SABCD là diện tích của hình vuông ABCD

SO là chiều cao từ điểm O xuống trung tâm của đáy ABCD

3.2. Một số bài tập ứng dụng

Bài tập 1: Cho khối chóp tứ giác SABCD với tất cả các cạnh có độ dài bằng a. Chứng minh rằng khối chóp SABCD là hình chóp tứ giác đều và tính thể tích của nó.

Hướng dẫn giải:

Vẽ đường thẳng SO vuông góc với mặt đáy ABCD

Vì SA = SB = SC = SD nên OA = OB = OC = OD

=> ABCD là hình thoi có đường tròn ngoại tiếp, do đó ABCD là hình vuông.

Ta có SA² + SB² = AB² + BC² = AC², nên tam giác ΔASC vuông tại S

Bài tập 2: Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD, với các cạnh đều có độ dài a.

Hướng dẫn giải:

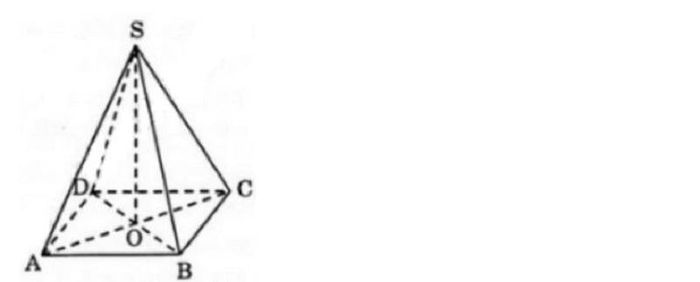
Xét hình chóp tứ giác đều S.ABCD với các cạnh có độ dài a.

Do đó, ABCD là một hình vuông với cạnh dài a, và SA = SB = SC = SD = a.

Điểm O là hình chiếu của điểm A lên mặt phẳng hình vuông ABCD, do đó, O là tâm của hình vuông ABCD.

Các đoạn OA, OB, OC, OD, và OS đều bằng nhau. Điểm O là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu là:

Bài tập 3: Nhiệm vụ là chia hình chóp tứ giác đều thành 8 hình chóp nhỏ bằng nhau:

Hướng dẫn giải: Để hoàn thành bài tập này, trước tiên hãy vẽ hình chóp và chia phần đáy thành 8 tam giác đều. Sau đó, chứng minh rằng các hình chóp có đỉnh là đỉnh của hình chóp ban đầu và đáy là các tam giác đã chia đều. Áp dụng kiến thức lý thuyết về hai tứ diện với các cạnh tương ứng bằng nhau thì chúng bằng nhau.

Vẽ hình

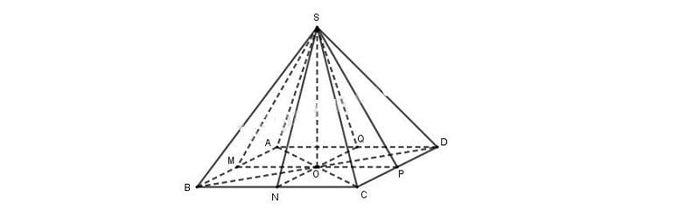
Gọi điểm O là giao điểm của AC với BD tại các điểm M, N, P, Q. Những điểm này là trung điểm của các đoạn AB, BC, CD, và DA. Do đó, các tam giác AOM, BOM, BON, CON, COP, DOP, DOQ và AOQ đều bằng nhau.

Chứng minh rằng các hình chóp S.AOM, S.BOM, S.BON, S.CON, S.COP, S.DOP, S.DOQ, và S.AOQ là bằng nhau.

Xem xét hai hình chóp S.AOM và S.BOM có

+ SA = SB; AO = BO; BM = AM.

+ Đồng thời, SO, SM và OM đều là các đoạn chung.

Vì vậy, hai tứ diện có các cạnh tương ứng bằng nhau thì chúng bằng nhau, dẫn đến việc có 8 hình chóp bằng nhau.

Trên đây là kiến thức về hình chóp tứ giác đều và phương pháp tính thể tích của nó cùng với các ví dụ cụ thể. Hy vọng bài viết đã cung cấp thông tin hữu ích cho bạn. Mytour xin chân thành cảm ơn!