In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and -sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and sinh(t) respectively.
Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics.
The basic hyperbolic functions are:[1]
- hyperbolic sine "sinh" (/ˈsɪŋ, ˈsɪntʃ, ˈʃaɪn/),[2]
- hyperbolic cosine "cosh" (/ˈkɒʃ, ˈkoʊʃ/),[3]
from which are derived:[4]
- hyperbolic tangent "tanh" (/ˈtæŋ, ˈtæntʃ, ˈθæn/),[5]
- hyperbolic cotangent "coth" (/ˈkɒθ, ˈkoʊθ/),[6][7]
- hyperbolic secant "sech" (/ˈsɛtʃ, ˈʃɛk/),[8]
- hyperbolic cosecant "csch" or "cosech" (/ˈkoʊsɛtʃ, ˈkoʊʃɛk/[3])
corresponding to the derived trigonometric functions.
The inverse hyperbolic functions are:
- inverse hyperbolic sine "arsinh" (also denoted "sinh−1", "asinh" or sometimes "arcsinh")[9][10][11]
- inverse hyperbolic cosine "arcosh" (also denoted "cosh−1", "acosh" or sometimes "arccosh")
- inverse hyperbolic tangent "artanh" (also denoted "tanh−1", "atanh" or sometimes "arctanh")
- inverse hyperbolic cotangent "arcoth" (also denoted "coth−1", "acoth" or sometimes "arccoth")
- inverse hyperbolic secant "arsech" (also denoted "sech−1", "asech" or sometimes "arcsech")
- inverse hyperbolic cosecant "arcsch" (also denoted "arcosech", "csch−1", "cosech−1","acsch", "acosech", or sometimes "arccsch" or "arccosech")
The hyperbolic functions take a real argument called a hyperbolic angle. The magnitude of a hyperbolic angle is the area of its hyperbolic sector to xy = 1. The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.
In complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. The hyperbolic sine and the hyperbolic cosine are entire functions. As a result, the other hyperbolic functions are meromorphic in the whole complex plane.
By Lindemann-Weierstrass theorem, the hyperbolic functions have a transcendental value for every non-zero algebraic value of the argument.[12]
The first known calculation of a hyperbolic trigonometry problem is attributed to Gerardus Mercator when issuing the Mercator map projection circa 1566. It requires tabulating solutions to a transcendental equation involving hyperbolic functions.[13]
The first to suggest a similarity between the sector of the circle and that of the hyperbola was Isaac Newton in his 1687 Principia Mathematica.[14]
Roger Cotes suggested to modify the trigonometric functions using the imaginary unit i = − 1 {displaystyle i={sqrt {-1}}}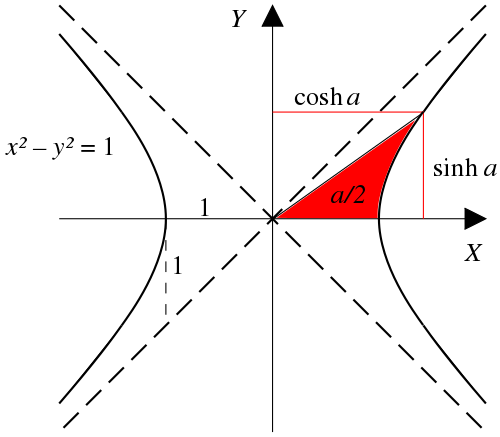 
to obtain an oblate spheroid from a prolate one.[14]
Hyperbolic functions were formally introduced in 1757 by Vincenzo Riccati.[14][13][15] Riccati used Sc. and Cc. (sinus/cosinus circulare) to refer to circular functions and Sh. and Ch. (sinus/cosinus hyperbolico) to refer to hyperbolic functions.[14] As early as 1759, Daviet de Foncenex showed the interchangeability of the trigonometric and hyperbolic functions using the imaginary unit and extended de Moivre's formula to hyperbolic functions.[15][14]
During the 1760s, Johann Heinrich Lambert systematized the use functions and provided exponential expressions in various publications.[14][15] Lambert credited Riccati for the terminology and names of the functions, but altered the abbreviations to those used today.[15][16]
There are various equivalent ways to define the hyperbolic functions.
In terms of the exponential function:[1][4]
- Hyperbolic sine: the odd part of the exponential function, that is, sinh x = e x − e − x 2 = e 2 x − 1 2 e x = 1 − e − 2 x 2 e − x . {displaystyle sinh x={frac {e^{x}-e^{-x}}{2}}={frac {e^{2x}-1}{2e^{x}}}={frac {1-e^{-2x}}{2e^{-x}}}.}
- Hyperbolic cosine: the even part of the exponential function, that is, cosh x = e x + e − x 2 = e 2 x + 1 2 e x = 1 + e − 2 x 2 e − x . {displaystyle cosh x={frac {e^{x}+e^{-x}}{2}}={frac {e^{2x}+1}{2e^{x}}}={frac {1+e^{-2x}}{2e^{-x}}}.}
- Hyperbolic tangent: tanh x = sinh x cosh x = e x − e − x e x + e − x = e 2 x − 1 e 2 x + 1 . {displaystyle tanh x={frac {sinh x}{cosh x}}={frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={frac {e^{2x}-1}{e^{2x}+1}}.}
- Hyperbolic cotangent: for x ≠ 0, coth x = cosh x sinh x = e x + e − x e x − e − x = e 2 x + 1 e 2 x − 1 . {displaystyle coth x={frac {cosh x}{sinh x}}={frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={frac {e^{2x}+1}{e^{2x}-1}}.}
- Hyperbolic secant: sech x = 1 cosh x = 2 e x + e − x = 2 e x e 2 x + 1 . {displaystyle operatorname {sech} x={frac {1}{cosh x}}={frac {2}{e^{x}+e^{-x}}}={frac {2e^{x}}{e^{2x}+1}}.}
- Hyperbolic cosecant: for x ≠ 0, csch x = 1 sinh x = 2 e x − e − x = 2 e x e 2 x − 1 . {displaystyle operatorname {csch} x={frac {1}{sinh x}}={frac {2}{e^{x}-e^{-x}}}={frac {2e^{x}}{e^{2x}-1}}.}
The hyperbolic functions may be defined as solutions of differential equations: The hyperbolic sine and cosine are the solution (s, c) of the system c ′ ( x ) = s ( x ) , s ′ ( x ) = c ( x ) , {displaystyle {begin{aligned}c'(x)&=s(x),s'(x)&=c(x),end{aligned}}} with the initial conditions s ( 0 ) = 0 , c ( 0 ) = 1. {displaystyle s(0)=0,c(0)=1.} 
The initial conditions make the solution unique; without them any pair of functions ( a e x + b e − x , a e x − b e − x ) {displaystyle (ae^{x}+be^{-x},ae^{x}-be^{-x})} would be a solution.
sinh(x) and cosh(x) are also the unique solution of the equation f ″(x) = f (x), such that f (0) = 1, f ′(0) = 0 for the hyperbolic cosine, and f (0) = 0, f ′(0) = 1 for the hyperbolic sine.
Hyperbolic functions may also be deduced from trigonometric functions with complex arguments:
- Hyperbolic sine:[1] sinh x = − i sin ( i x ) . {displaystyle sinh x=-isin(ix).}
- Hyperbolic cosine:[1] cosh x = cos ( i x ) . {displaystyle cosh x=cos(ix).}
- Hyperbolic tangent: tanh x = − i tan ( i x ) . {displaystyle tanh x=-itan(ix).}
- Hyperbolic cotangent: coth x = i cot ( i x ) . {displaystyle coth x=icot(ix).}
- Hyperbolic secant: sech x = sec ( i x ) . {displaystyle operatorname {sech} x=sec(ix).}
- Hyperbolic cosecant: csch x = i csc ( i x ) . {displaystyle operatorname {csch} x=icsc(ix).}
where i is the imaginary unit with i2 = −1.
The above definitions are related to the exponential definitions via Euler's formula (See § Hyperbolic functions for complex numbers below).
It can be shown that the area under the curve of the hyperbolic cosine (over a finite interval) is always equal to the arc length corresponding to that interval:[17] area = ∫ a b cosh x d x = ∫ a b 1 + ( d d x cosh x ) 2 d x = arc length. {displaystyle {text{area}}=int _{a}^{b}cosh x,dx=int _{a}^{b}{sqrt {1+left({frac {d}{dx}}cosh xright)^{2}}},dx={text{arc length.}}}
The hyperbolic tangent is the (unique) solution to the differential equation f ′ = 1 − f 2, with f (0) = 0.[18][19]
The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities. In fact, Osborn's rule[20] states that one can convert any trigonometric identity (up to but not including sinhs or implied sinhs of 4th degree) for θ {displaystyle theta } , 2 θ {displaystyle 2theta } , 3 θ {displaystyle 3theta } or θ {displaystyle theta } and φ {displaystyle varphi } into a hyperbolic identity, by:
- expanding it completely in terms of integral powers of sines and cosines,
- changing sine to sinh and cosine to cosh, and
- switching the sign of every term containing a product of two sinhs.
Odd and even functions: sinh ( − x ) = − sinh x cosh ( − x ) = cosh x {displaystyle {begin{aligned}sinh(-x)&=-sinh xcosh(-x)&=cosh xend{aligned}}}
Hence: tanh ( − x ) = − tanh x coth ( − x ) = − coth x sech ( − x ) = sech x csch ( − x ) = − csch x {displaystyle {begin{aligned}tanh(-x)&=-tanh xcoth(-x)&=-coth xoperatorname {sech} (-x)&=operatorname {sech} xoperatorname {csch} (-x)&=-operatorname {csch} xend{aligned}}}
Thus, cosh x and sech x are even functions; the others are odd functions.
arsech x = arcosh ( 1 x ) arcsch x = arsinh ( 1 x ) arcoth x = artanh ( 1 x ) {displaystyle {begin{aligned}operatorname {arsech} x&=operatorname {arcosh} left({frac {1}{x}}right)operatorname {arcsch} x&=operatorname {arsinh} left({frac {1}{x}}right)operatorname {arcoth} x&=operatorname {artanh} left({frac {1}{x}}right)end{aligned}}}
Hyperbolic sine and cosine satisfy: cosh x + sinh x = e x cosh x − sinh x = e − x {displaystyle {begin{aligned}cosh x+sinh x&=e^{x}cosh x-sinh x&=e^{-x}end{aligned}}}
which are analogous to Euler's formula, and
cosh 2 x − sinh 2 x = 1 {displaystyle cosh ^{2}x-sinh ^{2}x=1}
which is analogous to the Pythagorean trigonometric identity.
One also has sech 2 x = 1 − tanh 2 x csch 2 x = coth 2 x − 1 {displaystyle {begin{aligned}operatorname {sech} ^{2}x&=1-tanh ^{2}xoperatorname {csch} ^{2}x&=coth ^{2}x-1end{aligned}}}
for the other functions.
sinh ( x + y ) = sinh x cosh y + cosh x sinh y cosh ( x + y ) = cosh x cosh y + sinh x sinh y tanh ( x + y ) = tanh x + tanh y 1 + tanh x tanh y {displaystyle {begin{aligned}sinh(x+y)&=sinh xcosh y+cosh xsinh ycosh(x+y)&=cosh xcosh y+sinh xsinh ytanh(x+y)&={frac {tanh x+tanh y}{1+tanh xtanh y}}end{aligned}}} particularly cosh ( 2 x ) = sinh 2 x + cosh 2 x = 2 sinh 2 x + 1 = 2 cosh 2 x − 1 sinh ( 2 x ) = 2 sinh x cosh x tanh ( 2 x ) = 2 tanh x 1 + tanh 2 x {displaystyle {begin{aligned}cosh(2x)&=sinh ^{2}{x}+cosh ^{2}{x}=2sinh ^{2}x+1=2cosh ^{2}x-1sinh(2x)&=2sinh xcosh xtanh(2x)&={frac {2tanh x}{1+tanh ^{2}x}}end{aligned}}}
Also: sinh x + sinh y = 2 sinh ( x + y 2 ) cosh ( x − y 2 ) cosh x + cosh y = 2 cosh ( x + y 2 ) cosh ( x − y 2 ) {displaystyle {begin{aligned}sinh x+sinh y&=2sinh left({frac {x+y}{2}}right)cosh left({frac {x-y}{2}}right)cosh x+cosh y&=2cosh left({frac {x+y}{2}}right)cosh left({frac {x-y}{2}}right)end{aligned}}}
sinh ( x − y ) = sinh x cosh y − cosh x sinh y cosh ( x − y ) = cosh x cosh y − sinh x sinh y tanh ( x − y ) = tanh x − tanh y 1 − tanh x tanh y {displaystyle {begin{aligned}sinh(x-y)&=sinh xcosh y-cosh xsinh ycosh(x-y)&=cosh xcosh y-sinh xsinh ytanh(x-y)&={frac {tanh x-tanh y}{1-tanh xtanh y}}end{aligned}}}
Also:[21] sinh x − sinh y = 2 cosh ( x + y 2 ) sinh ( x − y 2 ) cosh x − cosh y = 2 sinh ( x + y 2 ) sinh ( x − y 2 ) {displaystyle {begin{aligned}sinh x-sinh y&=2cosh left({frac {x+y}{2}}right)sinh left({frac {x-y}{2}}right)cosh x-cosh y&=2sinh left({frac {x+y}{2}}right)sinh left({frac {x-y}{2}}right)end{aligned}}}
sinh ( x 2 ) = sinh x 2 ( cosh x + 1 ) = sgn x cosh x − 1 2 cosh ( x 2 ) = cosh x + 1 2 tanh ( x 2 ) = sinh x cosh x + 1 = sgn x cosh x − 1 cosh x + 1 = e x − 1 e x + 1 {displaystyle {begin{aligned}sinh left({frac {x}{2}}right)&={frac {sinh x}{sqrt {2(cosh x+1)}}}&&=operatorname {sgn} x,{sqrt {frac {cosh x-1}{2}}}[6px]cosh left({frac {x}{2}}right)&={sqrt {frac {cosh x+1}{2}}}[6px]tanh left({frac {x}{2}}right)&={frac {sinh x}{cosh x+1}}&&=operatorname {sgn} x,{sqrt {frac {cosh x-1}{cosh x+1}}}={frac {e^{x}-1}{e^{x}+1}}end{aligned}}}
where sgn is the sign function.
If x ≠ 0, then[22]
tanh ( x 2 ) = cosh x − 1 sinh x = coth x − csch x {displaystyle tanh left({frac {x}{2}}right)={frac {cosh x-1}{sinh x}}=coth x-operatorname {csch} x}
sinh 2 x = 1 2 ( cosh 2 x − 1 ) cosh 2 x = 1 2 ( cosh 2 x + 1 ) {displaystyle {begin{aligned}sinh ^{2}x&={tfrac {1}{2}}(cosh 2x-1)cosh ^{2}x&={tfrac {1}{2}}(cosh 2x+1)end{aligned}}}
The following inequality is useful in statistics:[23] cosh ( t ) ≤ e t 2 / 2 . {displaystyle operatorname {cosh} (t)leq e^{t^{2}/2}.}
It can be proved by comparing the Taylor series of the two functions term by term.
arsinh ( x ) = ln ( x + x 2 + 1 ) arcosh ( x ) = ln ( x + x 2 − 1 ) x ≥ 1 artanh ( x ) = 1 2 ln ( 1 + x 1 − x ) | x | < 1 arcoth ( x ) = 1 2 ln ( x + 1 x − 1 ) | x | > 1 arsech ( x ) = ln ( 1 x + 1 x 2 − 1 ) = ln ( 1 + 1 − x 2 x ) 0 < x ≤ 1 arcsch ( x ) = ln ( 1 x + 1 x 2 + 1 ) x ≠ 0 {displaystyle {begin{aligned}operatorname {arsinh} (x)&=ln left(x+{sqrt {x^{2}+1}}right)operatorname {arcosh} (x)&=ln left(x+{sqrt {x^{2}-1}}right)&&xgeq 1operatorname {artanh} (x)&={frac {1}{2}}ln left({frac {1+x}{1-x}}right)&&|x|<1operatorname {arcoth} (x)&={frac {1}{2}}ln left({frac {x+1}{x-1}}right)&&|x|>1operatorname {arsech} (x)&=ln left({frac {1}{x}}+{sqrt {{frac {1}{x^{2}}}-1}}right)=ln left({frac {1+{sqrt {1-x^{2}}}}{x}}right)&&0<xleq 1operatorname {arcsch} (x)&=ln left({frac {1}{x}}+{sqrt {{frac {1}{x^{2}}}+1}}right)&&xneq 0end{aligned}}}
d d x sinh x = cosh x d d x cosh x = sinh x d d x tanh x = 1 − tanh 2 x = sech 2 x = 1 cosh 2 x d d x coth x = 1 − coth 2 x = − csch 2 x = − 1 sinh 2 x x ≠ 0 d d x sech x = − tanh x sech x d d x csch x = − coth x csch x x ≠ 0 {displaystyle {begin{aligned}{frac {d}{dx}}sinh x&=cosh x{frac {d}{dx}}cosh x&=sinh x{frac {d}{dx}}tanh x&=1-tanh ^{2}x=operatorname {sech} ^{2}x={frac {1}{cosh ^{2}x}}{frac {d}{dx}}coth x&=1-coth ^{2}x=-operatorname {csch} ^{2}x=-{frac {1}{sinh ^{2}x}}&&xneq 0{frac {d}{dx}}operatorname {sech} x&=-tanh xoperatorname {sech} x{frac {d}{dx}}operatorname {csch} x&=-coth xoperatorname {csch} x&&xneq 0end{aligned}}} d d x arsinh x = 1 x 2 + 1 d d x arcosh x = 1 x 2 − 1 1 < x d d x artanh x = 1 1 − x 2 | x | < 1 d d x arcoth x = 1 1 − x 2 1 < | x | d d x arsech x = − 1 x 1 − x 2 0 < x < 1 d d x arcsch x = − 1 | x | 1 + x 2 x ≠ 0 {displaystyle {begin{aligned}{frac {d}{dx}}operatorname {arsinh} x&={frac {1}{sqrt {x^{2}+1}}}{frac {d}{dx}}operatorname {arcosh} x&={frac {1}{sqrt {x^{2}-1}}}&&1<x{frac {d}{dx}}operatorname {artanh} x&={frac {1}{1-x^{2}}}&&|x|<1{frac {d}{dx}}operatorname {arcoth} x&={frac {1}{1-x^{2}}}&&1<|x|{frac {d}{dx}}operatorname {arsech} x&=-{frac {1}{x{sqrt {1-x^{2}}}}}&&0<x<1{frac {d}{dx}}operatorname {arcsch} x&=-{frac {1}{|x|{sqrt {1+x^{2}}}}}&&xneq 0end{aligned}}}
Each of the functions sinh and cosh is equal to its second derivative, that is: d 2 d x 2 sinh x = sinh x {displaystyle {frac {d^{2}}{dx^{2}}}sinh x=sinh x} d 2 d x 2 cosh x = cosh x . {displaystyle {frac {d^{2}}{dx^{2}}}cosh x=cosh x,.}
All functions with this property are linear combinations of sinh and cosh, in particular the exponential functions e x {displaystyle e^{x}} and e − x {displaystyle e^{-x}} .[24]
∫ sinh ( a x ) d x = a − 1 cosh ( a x ) + C ∫ cosh ( a x ) d x = a − 1 sinh ( a x ) + C ∫ tanh ( a x ) d x = a − 1 ln ( cosh ( a x ) ) + C ∫ coth ( a x ) d x = a − 1 ln | sinh ( a x ) | + C ∫ sech ( a x ) d x = a − 1 arctan ( sinh ( a x ) ) + C ∫ csch ( a x ) d x = a − 1 ln | tanh ( a x 2 ) | + C = a − 1 ln | coth ( a x ) − csch ( a x ) | + C = − a − 1 arcoth ( cosh ( a x ) ) + C {displaystyle {begin{aligned}int sinh(ax),dx&=a^{-1}cosh(ax)+Cint cosh(ax),dx&=a^{-1}sinh(ax)+Cint tanh(ax),dx&=a^{-1}ln(cosh(ax))+Cint coth(ax),dx&=a^{-1}ln left|sinh(ax)right|+Cint operatorname {sech} (ax),dx&=a^{-1}arctan(sinh(ax))+Cint operatorname {csch} (ax),dx&=a^{-1}ln left|tanh left({frac {ax}{2}}right)right|+C=a^{-1}ln left|coth left(axright)-operatorname {csch} left(axright)right|+C=-a^{-1}operatorname {arcoth} left(cosh left(axright)right)+Cend{aligned}}}
The following integrals can be proved using hyperbolic substitution: ∫ 1 a 2 + u 2 d u = arsinh ( u a ) + C ∫ 1 u 2 − a 2 d u = sgn u arcosh | u a | + C ∫ 1 a 2 − u 2 d u = a − 1 artanh ( u a ) + C u 2 < a 2 ∫ 1 a 2 − u 2 d u = a − 1 arcoth ( u a ) + C u 2 > a 2 ∫ 1 u a 2 − u 2 d u = − a − 1 arsech | u a | + C ∫ 1 u a 2 + u 2 d u = − a − 1 arcsch | u a | + C {displaystyle {begin{aligned}int {{frac {1}{sqrt {a^{2}+u^{2}}}},du}&=operatorname {arsinh} left({frac {u}{a}}right)+Cint {{frac {1}{sqrt {u^{2}-a^{2}}}},du}&=operatorname {sgn} {u}operatorname {arcosh} left|{frac {u}{a}}right|+Cint {frac {1}{a^{2}-u^{2}}},du&=a^{-1}operatorname {artanh} left({frac {u}{a}}right)+C&&u^{2}<a^{2}int {frac {1}{a^{2}-u^{2}}},du&=a^{-1}operatorname {arcoth} left({frac {u}{a}}right)+C&&u^{2}>a^{2}int {{frac {1}{u{sqrt {a^{2}-u^{2}}}}},du}&=-a^{-1}operatorname {arsech} left|{frac {u}{a}}right|+Cint {{frac {1}{u{sqrt {a^{2}+u^{2}}}}},du}&=-a^{-1}operatorname {arcsch} left|{frac {u}{a}}right|+Cend{aligned}}}
where C is the constant of integration.
It is possible to express explicitly the Taylor series at zero (or the Laurent series, if the function is not defined at zero) of the above functions.
sinh x = x + x 3 3 ! + x 5 5 ! + x 7 7 ! + ⋯ = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! {displaystyle sinh x=x+{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}+{frac {x^{7}}{7!}}+cdots =sum _{n=0}^{infty }{frac {x^{2n+1}}{(2n+1)!}}} This series is convergent for every complex value of x. Since the function sinh x is odd, only odd exponents for x occur in its Taylor series.
cosh x = 1 + x 2 2 ! + x 4 4 ! + x 6 6 ! + ⋯ = ∑ n = 0 ∞ x 2 n ( 2 n ) ! {displaystyle cosh x=1+{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}+{frac {x^{6}}{6!}}+cdots =sum _{n=0}^{infty }{frac {x^{2n}}{(2n)!}}} This series is convergent for every complex value of x. Since the function cosh x is even, only even exponents for x occur in its Taylor series.
The sum of the sinh and cosh series is the infinite series expression of the exponential function.
The following series are followed by a description of a subset of their domain of convergence, where the series is convergent and its sum equals the function. tanh x = x − x 3 3 + 2 x 5 15 − 17 x 7 315 + ⋯ = ∑ n = 1 ∞ 2 2 n ( 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! , | x | < π 2 coth x = x − 1 + x 3 − x 3 45 + 2 x 5 945 + ⋯ = ∑ n = 0 ∞ 2 2 n B 2 n x 2 n − 1 ( 2 n ) ! , 0 < | x | < π sech x = 1 − x 2 2 + 5 x 4 24 − 61 x 6 720 + ⋯ = ∑ n = 0 ∞ E 2 n x 2 n ( 2 n ) ! , | x | < π 2 csch x = x − 1 − x 6 + 7 x 3 360 − 31 x 5 15120 + ⋯ = ∑ n = 0 ∞ 2 ( 1 − 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! , 0 < | x | < π {displaystyle {begin{aligned}tanh x&=x-{frac {x^{3}}{3}}+{frac {2x^{5}}{15}}-{frac {17x^{7}}{315}}+cdots =sum _{n=1}^{infty }{frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},qquad left|xright|<{frac {pi }{2}}coth x&=x^{-1}+{frac {x}{3}}-{frac {x^{3}}{45}}+{frac {2x^{5}}{945}}+cdots =sum _{n=0}^{infty }{frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},qquad 0<left|xright|<pi operatorname {sech} x&=1-{frac {x^{2}}{2}}+{frac {5x^{4}}{24}}-{frac {61x^{6}}{720}}+cdots =sum _{n=0}^{infty }{frac {E_{2n}x^{2n}}{(2n)!}},qquad left|xright|<{frac {pi }{2}}operatorname {csch} x&=x^{-1}-{frac {x}{6}}+{frac {7x^{3}}{360}}-{frac {31x^{5}}{15120}}+cdots =sum _{n=0}^{infty }{frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},qquad 0<left|xright|<pi end{aligned}}}
where:
- B n {displaystyle B_{n}} is the nth Bernoulli number
- E n {displaystyle E_{n}} is the nth Euler number
The following expansions are valid in the whole complex plane:
sinh x = x ∏ n = 1 ∞ ( 1 + x 2 n 2 π 2 ) = x 1 − x 2 2 ⋅ 3 + x 2 − 2 ⋅ 3 x 2 4 ⋅ 5 + x 2 − 4 ⋅ 5 x 2 6 ⋅ 7 + x 2 − ⋱ {displaystyle sinh x=xprod _{n=1}^{infty }left(1+{frac {x^{2}}{n^{2}pi ^{2}}}right)={cfrac {x}{1-{cfrac {x^{2}}{2cdot 3+x^{2}-{cfrac {2cdot 3x^{2}}{4cdot 5+x^{2}-{cfrac {4cdot 5x^{2}}{6cdot 7+x^{2}-ddots }}}}}}}}} cosh x = ∏ n = 1 ∞ ( 1 + x 2 ( n − 1 / 2 ) 2 π 2 ) = 1 1 − x 2 1 ⋅ 2 + x 2 − 1 ⋅ 2 x 2 3 ⋅ 4 + x 2 − 3 ⋅ 4 x 2 5 ⋅ 6 + x 2 − ⋱ {displaystyle cosh x=prod _{n=1}^{infty }left(1+{frac {x^{2}}{(n-1/2)^{2}pi ^{2}}}right)={cfrac {1}{1-{cfrac {x^{2}}{1cdot 2+x^{2}-{cfrac {1cdot 2x^{2}}{3cdot 4+x^{2}-{cfrac {3cdot 4x^{2}}{5cdot 6+x^{2}-ddots }}}}}}}}} tanh x = 1 1 x + 1 3 x + 1 5 x + 1 7 x + ⋱ {displaystyle tanh x={cfrac {1}{{cfrac {1}{x}}+{cfrac {1}{{cfrac {3}{x}}+{cfrac {1}{{cfrac {5}{x}}+{cfrac {1}{{cfrac {7}{x}}+ddots }}}}}}}}}The hyperbolic functions represent an expansion of trigonometry beyond the circular functions. Both types depend on an argument, either circular angle or hyperbolic angle.
Since the area of a circular sector with radius r and angle u (in radians) is r2u/2, it will be equal to u when r = √2. In the diagram, such a circle is tangent to the hyperbola xy = 1 at (1,1). The yellow sector depicts an area and angle magnitude. Similarly, the yellow and red regions together depict a hyperbolic sector with area corresponding to hyperbolic angle magnitude.
The legs of the two right triangles with hypotenuse on the ray defining the angles are of length √2 times the circular and hyperbolic functions.
The hyperbolic angle is an invariant measure with respect to the squeeze mapping, just as the circular angle is invariant under rotation.[25]
The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic functions that does not involve complex numbers.
The graph of the function a cosh(x/a) is the catenary, the curve formed by a uniform flexible chain, hanging freely between two fixed points under uniform gravity.
The decomposition of the exponential function in its even and odd parts gives the identities e x = cosh x + sinh x , {displaystyle e^{x}=cosh x+sinh x,} and e − x = cosh x − sinh x . {displaystyle e^{-x}=cosh x-sinh x.} Combined with Euler's formula e i x = cos x + i sin x , {displaystyle e^{ix}=cos x+isin x,} this gives e x + i y = ( cosh x + sinh x ) ( cos y + i sin y ) {displaystyle e^{x+iy}=(cosh x+sinh x)(cos y+isin y)} for the general complex exponential function.
Additionally, e x = 1 + tanh x 1 − tanh x = 1 + tanh x 2 1 − tanh x 2 {displaystyle e^{x}={sqrt {frac {1+tanh x}{1-tanh x}}}={frac {1+tanh {frac {x}{2}}}{1-tanh {frac {x}{2}}}}}
Hyperbolic functions in the complex plane sinh ( z ) {displaystyle sinh(z)} cosh ( z ) {displaystyle cosh(z)} tanh ( z ) {displaystyle tanh(z)} coth ( z ) {displaystyle coth(z)} sech ( z ) {displaystyle operatorname {sech} (z)} csch ( z ) {displaystyle operatorname {csch} (z)}Since the exponential function can be defined for any complex argument, we can also extend the definitions of the hyperbolic functions to complex arguments. The functions sinh z and cosh z are then holomorphic.
Relationships to ordinary trigonometric functions are given by Euler's formula for complex numbers: e i x = cos x + i sin x e − i x = cos x − i sin x {displaystyle {begin{aligned}e^{ix}&=cos x+isin xe^{-ix}&=cos x-isin xend{aligned}}} so: cosh ( i x ) = 1 2 ( e i x + e − i x ) = cos x sinh ( i x ) = 1 2 ( e i x − e − i x ) = i sin x cosh ( x + i y ) = cosh ( x ) cos ( y ) + i sinh ( x ) sin ( y ) sinh ( x + i y ) = sinh ( x ) cos ( y ) + i cosh ( x ) sin ( y ) tanh ( i x ) = i tan x cosh x = cos ( i x ) sinh x = − i sin ( i x ) tanh x = − i tan ( i x ) {displaystyle {begin{aligned}cosh(ix)&={frac {1}{2}}left(e^{ix}+e^{-ix}right)=cos xsinh(ix)&={frac {1}{2}}left(e^{ix}-e^{-ix}right)=isin xcosh(x+iy)&=cosh(x)cos(y)+isinh(x)sin(y)sinh(x+iy)&=sinh(x)cos(y)+icosh(x)sin(y)tanh(ix)&=itan xcosh x&=cos(ix)sinh x&=-isin(ix)tanh x&=-itan(ix)end{aligned}}}
Thus, hyperbolic functions are periodic with respect to the imaginary component, with period 2 π i {displaystyle 2pi i} ( π i {displaystyle pi i} for hyperbolic tangent and cotangent).
- e (mathematical constant)
- Equal incircles theorem, based on sinh
- Hyperbolastic functions
- Hyperbolic growth
- Inverse hyperbolic functions
- List of integrals of hyperbolic functions
- Poinsot's spirals
- Sigmoid function
- Soboleva modified hyperbolic tangent
- Trigonometric functions
- "Hyperbolic functions", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Hyperbolic functions on PlanetMath
- GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions (Java Web Start)
- Web-based calculator of hyperbolic functions
